Grids are great for tactical gameplay of turn-based games because they allow discrete movement steps. That means that you can bind positioning to other resources such as movement points, action points, food, etc. Grids divide the infinite variety of movement options into a few specific ones, which can be considered separately by the player’s tactical mind. The most popular grid types are hexes and squares. But what about triangles?
Types of Grids: Comparison
We are perfectly familiar with square and hex grids, as most turn-based games use one of them. Both have upsides and downsides. I will go through each of these and include the triangle grid in comparison.

Visuals
Square grids will contribute to visuals for non-natural environments, such as towns, dungeons, streets, and building interiors.
Hex grids look nice with natural environments instead, improving the realism of curvy things, such as islands, mountains, small roads, etc.
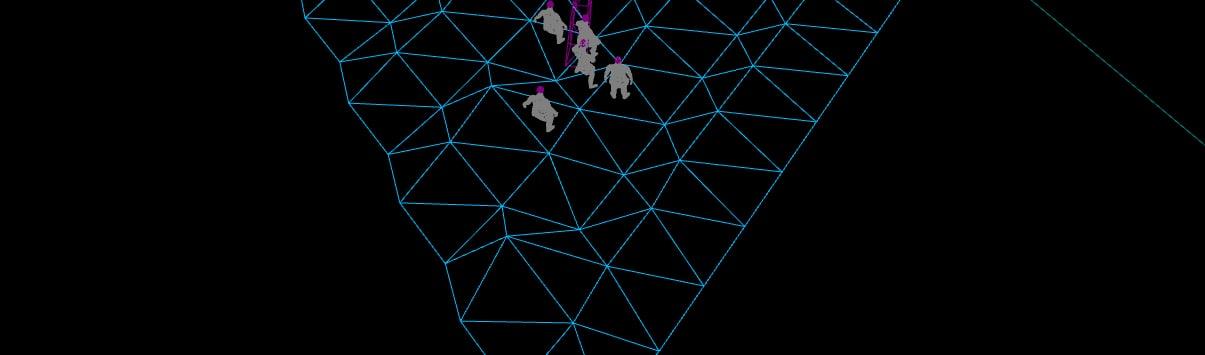
In the case with looks, triangle grids lie in between: like squares, they allow straight lines and walls without half-tiles, and like hexes, they allow more curvy environments. In fact, triangle grids contain both in itself! You can even have rhombus (huge) and hex (colossal) creatures on top of the triangle grid, like this:

On top of that, it has a bonus: like the square grid, it can contain bigger and smaller grids in itself.
The only visual downside before the square grid is that it can’t express rectangle buildings. In this case, the same cheat from the hex grid can be used: use half tiles. A blocking object (wall) goes through half of the tile and the tile is blocked completely.

There are also two special cases that make triangles shine. The first is line formations. When the second row of spearmen/riflemen stays between the first, like on the picture above, they can attack enemy formation too without a friend obstructing the view.
So it’s possible to directly represent lines of soldiers on triangular grids; formations will also have the ability to rotate in 6 directions. But this point applies to hex grids too, it’s just that the second row will be further away from enemies, and with triangles, enemies in front of the formations are diagonally-adjacent to the second row. I’ll tell you more about diagonals and diagonal distances in a minute.
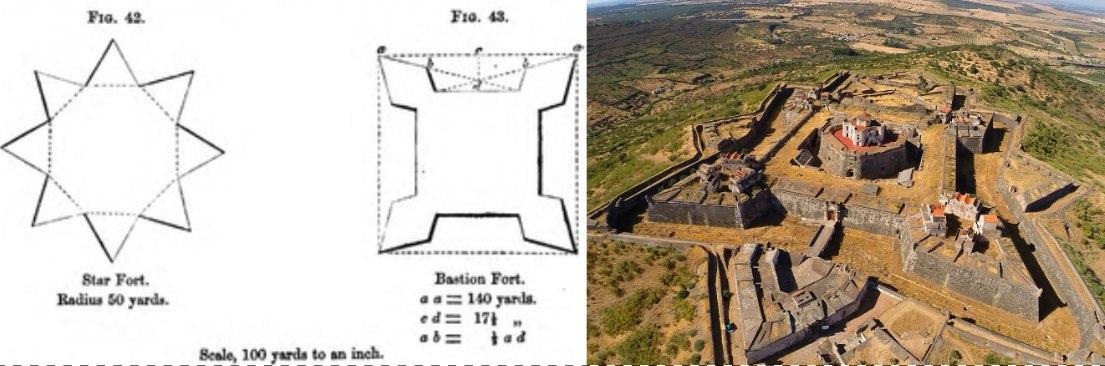
Another thing is citadels/bastions. These angles allow more convenient defenses, and fortifications were often built this way throughout history. In Colossal Citadels I made walls and houses follow the triangular grid and I love how these procedurally-generated castles turned out:

Directions and Adjacent Tiles
The number of tactical options (movements, attacks, ranged straight-line attacks) depends on the type of grid. It also depends on whether or not you allow diagonal directions. Let’s count how many non-diagonal directions each grid type allows:

- Square grid: 4 adjacent tiles, 4 directions
- Hex grid: 6 adjacent tiles, 6 directions
- Triangle grid: 3 adjacent tiles, 6 directions
Restricting the number of options would make sense in a tight puzzle-like tactics game, and in bigger strategy games you might want to increase the variety of options to depend less on micro tactics on movement.
Directions And Adjacent Tiles: Diagonals
Some games increase these numbers by allowing diagonal tiles and directions. This is where triangle grids overcome other variants!
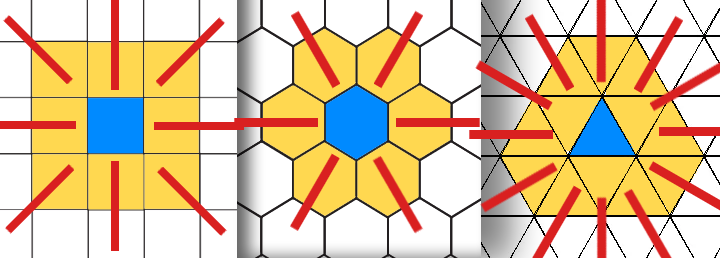
- Square grid: 8 adjacent tiles, 8 directions
- Hex grid: 6 adjacent tiles, 6 directions
- Triangle grid: 12 adjacent tiles, 12 directions
So, if you want to have more options, triangle grids with diagonals are a good choice. Ranged “line” attacks also look slightly better because they’re not alternating as with the hex grids; be sure to highlight the lines in 6 straight diagonals, or it will look not so good.
Distances

- Hex grids are very good at estimating the closest path - you can naturally see the closest point.
- Square grids without diagonals are not so convenient, but distances are always easy to calculate.
- Triangle grids without diagonals are fine, but there is an issue when you have an opposing triangle: it takes 3 steps to move to it. This might look weird and unnatural. We can fix this by introducing diagonals: allow jumping to the opposing triangle at the cost of 2 instead of three. Then, triangular grid becomes convenient to use and more realistic:
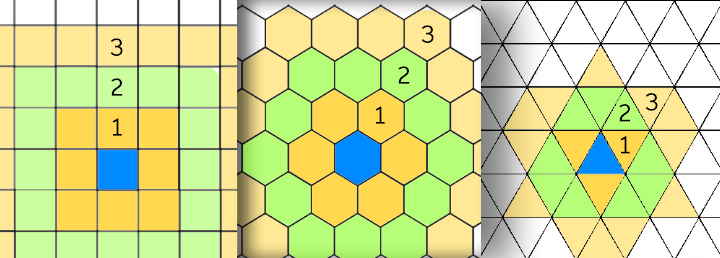
You can find calculating functions for all distances (and explanations) in the end of this article. By the way, I believe I was the first to mention this and the next kind of triangle diagonal distances in the internet here - it links to another cool article by BorisTheBrave. But these grids are simple stuff in my opinion, and most possibly, board game developers who explored triangle grids already have considered it long ago.
So, this way of calculating distance is quite fine for movements, but for less edgy shapes (for example, buildings), you might want to have something even simpler: full diagonal distances. Treat all tiles that touch the current triangle with one of the vertices as a distance of 1.
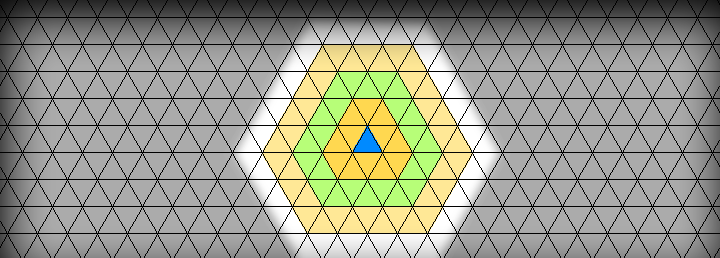
Unfortunately, this approach is not a panacea: it’s not that beautiful for movement, because a moving unit can cheat a little bit and cover up to two times more tiles than in previous distance measures! Can you figure out how? But this type of distance is very good for ranged attacks and zones! So, I would suggest using either the previous formula, or both: full diagonals for ranges and diagonal shortcut for movements.
Heightmap Terrains
This is not a gameplay point, but it’s still worth mentioning. There is a way of drawing terrain meshes with triangles instead of quads. This way can save some percentage of triangle count and fixes some other issues automatically. If terrain tiles are tied to gameplay, this is going to look interesting. I’ve not seen a triangular grid voxel minecraft-like game yet!
How To Use Triangular Grid
Red Blob Games’s article provides a lot of thoughts on representations of triangle grid, but I’ll just use the best one and supply it with a lot of common useful operations on it.
Coordinate Representation
The most convenient option is to represent it as square grid coordinates PLUS a number that means half-square - 0 or 1.
struct Pos
{
int x, y, s;
};
Conversions
Conversions between index, coordinates, and 2D world coordinates are going to be the most common operations.
Index <-> Coordinates
int toIndex(const Pos& pos, int gridWidth)
{
return pos.x * 2 + pos.y * gridWidth * 2 + pos.s;
}
Pos fromIndex(int i, int gridWidth)
{
return Pos{(i / 2) % gridWidth, (i / 2) / gridWidth, i % 2};
}
World <-> Coordinates
struct Vec2
{
float x, y;
};
We will need some constants for representing tile size in world space. I use these:
namespace TriangleConstants
{
const float Height = 150.f;
const float Side = 173.20508075689f;
}
Vec2 gridToWorld(
const Pos& pos,
float worldspaceTriangleSide,
float worldspaceTriangleHeight)
{
return Vec2{
pos.x * worldspaceTriangleSide + pos.y * worldspaceTriangleSide / 2.f,
pos.y * worldspaceTriangleHeight
};
}
Pos worldToGrid(const Vec2& pos)
{
float y = std::get<1>(pos) / TriangleConstants::Height;
float x = std::get<0>(pos) / TriangleConstants::Side - y / 2.f;
bool s = (x - floorf(x) + y - floorf(y)) > 1.f;
return Pos{int(x), int(y), int(s)};
}
Trianglular Grid <-> Square Grid
It’s just as simple as taking x and y components and adding or removing third coordinate from them.
Triangle Tile Distance
To calculate simple tile distance you can use Manhattan distance with addition of third component difference.
int distance(const Pos& a, const Pos& b)
{
auto dx = a.x - b.x;
auto dy = a.y - b.y;
auto ds = a.s - b.s;
return abs(dx) + abs(dy) + abs(dx + dy + ds);
}
The logic behind this formula is that first you need to convert your coordinates to intermediate representation (adx, adx, adz), that reflects distances from initial point on three axes, each one parallel to one side of a triangle. Since it is just a taxicab distance, you need to just sum three components up.
Convenient distance functions are a bit more complex:
Diagonal Triangle Tile Distance (Shortcuts)
To allow movement through diagonal, you have to subtract the minimum of three distance components from the previous formula. Why is that and how did I find this? That information is lost… Probably, I just noticed it from staring at triangular grid for too long.
int triangleDistanceDiagonal(const TilePosition& a, const TilePosition& b)
{
auto dx = a.x - b.x;
auto dy = a.y - b.y;
auto ds = a.s - b.s;
auto adx = abs(dx);
auto ady = abs(dy);
auto adz = abs(dx + dy + ds);
auto m = std::min({adx, ady, adz});
return adx + ady + adz - m;
}
Diagonal Triangle Tile Distance (Full)
This is much simpler. To treat all diagonal tiles as distance one, you have to find maximum of all three components instead:
int triangleDistanceFullDiagonal(const TilePosition& a, const TilePosition& b)
{
auto dx = a.x - b.x;
auto dy = a.y - b.y;
auto ds = a.s - b.s;
auto adx = abs(dx);
auto ady = abs(dy);
auto adz = abs(dx + dy + ds);
return std::max({adx, ady, adz});
}
Source Code
All these functions plus some lesser ones, for example, calculating adjacent coordinate with or without diagonals, are included in my tiny header library. Feel free to use it, it’s published under CC0.
Conclusion
Triangular grids are a fantastic option too. As far as I know, there are no released games that make use of triangle grids yet. Maybe my project (from the screenshots above) will be the first? There are some board games - someone even tried to play Go on triangular grids.
However, the design of my game doesn’t need precise movement controls. You still play with grids with abilities and town-building, but the positioning of creatures is automatic. So, the space for classic turn-based tactics on triangle grids will be still open.
There are also other bizarre and irregular grid types. I can see some interesting gameplay ideas coming out from these, e.g. buildings can only go on big tiles, or smaller tiles are for “upgrades” that apply to big tiles, and so on.
